14 - Huffman-kódolás¶

Ebben a leckében (főleg a built-in kollekció osztályok használatával) implementáljuk a Huffman-kódolás néven hallgató szövegtömörítő algoritmust, írunk hozzá dekódert is.

az algoritmus¶

A Huffman-kódolás azon az elven működik, hogy az input szövegben minden karakterhez egy bináris stringet rendel úgy, hogy a gyakoribb karakterek rövidebb, a ritkábbak hosszabb kódot kapjanak, és ha csak egymás után rakjuk a kódszavakat, akkor könnyen visszafejthető legyen.

Konkrétabban:

először megszámoljuk minden karakterről a szövegben, hogy hányszor fordul elő
eztán kódfákat építünk, ami egy bináris (de nem kereső) fa és a következőképp néz ki:
- a levelekben, akiknek nincs gyereke, egy karaktert tárolunk adatként
- a belső csúcsok mindegyikének van egy nullás és egy egyes fia (ugyanaz, mint a bal/jobb, csak 0/1), amik szintén kódfák
- és minden csúcsnak van egy súlya is, ami egy pozitív egész szám
alapból minden karakterből építünk egy-egy egycsúcsú kódfát, a tárolt karakter maga a karakter lesz, a súly pedig a karakter gyakorisága a szövegben
a kapott kódfákat beöntjük egy kollekcióba, mondjuk egy kódfa-halmazba
ezután amíg a kódfahalmazban van több kódfa (a cél, hogy egyetlen kódfánk legyen, amiben benne az összes karakter, az elején sok kódfánk van, mindhez külön-külön egy-egy fa):
- kivesszük a halmazból a két minimális súlyú kódfát (a kódfa súlya a gyökerének a súlya), legyenek ők mondjuk t1 és t2
- helyettük meg beteszünk egy olyan kódfát, melynek nullás fia t1, egyes fia t2, gyökérsúlya pedig t1 és t2 gyökérsúlyainak összege
ha már csak egy elem van a kódfahalmazunkban, akkor megvan a szótárunk, amivel elkódolhatjuk a szöveget.

A kódolás:

minden karaktert a hozzá mint levélhez vezető úton összeolvasott bitsorozat kódol: pl. ha az a betűhöz a gyökérből a nullás-egyes-egyes-nullás gyereksorozaton keresztül jutunk el (tehát pl 4 mélyen van a fában), akkor őt a 0110 fogja kódolni
hogy ez gyorsan menjen, ezt összegyűjtjük egy karakter -> bináris sorozat Mapbe, mielőtt megkezdjük a kódolást
ha megvan a map, csak minden karaktert ki kell cserélnünk a neki megfeleltetett bináris stringre a szövegben
eztán nyolcasával lesznek belőle Byteok
ha nem osztható a szöveg elkódolt alakja 8-cal, valahogy azonosítanunk kell a szemetet a bitstream végén: ezért az egész sorozat első három bitje azt a 0..7 közti számot fogja reprezentálni, hogy hány bit trash a sorozat legvégén
ha ténylegesen egy file-tömörítőt írnánk, a szótárat is ki kéne írnunk valamilyen formátumban, ettől most eltekintünk

A dekódolás:

beolvassuk a karakterláncot kódoló bitstreamet, és csak a gyökérből elindulva mindig a soron következő bit által mutatott gyerek felé megyünk. Ha egy levélhez érünk, kiírjuk a karaktert és visszaugrunk a kódfa gyökeréhez
az elején a 0..7 szám dekódolása, és a stream végéről az ennyi trash bit eldobása is része a feladatnak

példa¶

Ha például az eredeti szövegben a betűből van 3, b-ből 6, c-ből 4, d-ből 10 és e-ből 11, akkor a kódfa építés így fut:

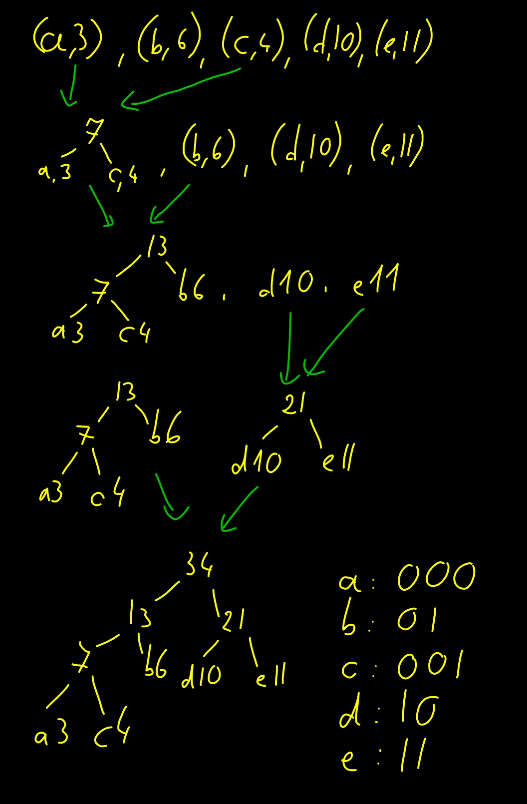
huffman

Először öt egypontú fa van a halmazban (első sor)
Eztán mivel a 3-as és a 4-es súlyúak a legkönnyebbek, ezeket összevonjuk egy 3+4=7 súlyú fába (második sor)
Most a 6 és a 7 súlyú fák a legkönnyebbek, ezeket vonjuk össze, lesz egy 13 súlyú fa helyettük
Most a 10 és 11 súlyúak a legkönnyebbek, ezekből lesz egy 21 súlyú
Végül egyetlen fánk marad, egy 34 súlyú.

Ha balra vannak a nullás gyerekek és jobbra az egyesek a képen, akkor pl. az a kódja 000 lesz, mert a gyökérből az a címkéjű levélhez három nullás gyereken át jutunk el. A d kódja pedig 10, mert először egy 1-es, majd egy 0-s gyerek felé kell mennünk, hogy odajussunk.

Eztán már csak annyi dolgunk van a szöveggel, hogy

kiszámoljuk, milyen hosszú lesz az eredménynek a ,,szöveges'' része: 3 darab 3 hosszú az a-nak, 6 darab 2 hosszú a b-nek, 4 darab 3 hosszú a c-nek, 10 darab 2 hosszú d-nek és 11 darab 2 hosszú az e-nek, ez összesen 3*3 + 6*2 + 4*3 + 10*2 + 11*2 = 9 + 12 + 12 + 20 + 22 = 73 bit,
plusz az elején a 0-7et tároló 3 bit, az 76 bit,
ami azt jelenti, hogy 10 byteot fogunk felhasználni, az 80 bit, és ebből 4 lesz a ,,trash'' a végén
tehát kiírjuk a 100 bitsorozatot (ami a 4-et jelenti), és ezután minden betű helyére az őt kódoló biteket, nyolcasával byteokba szervezve.

Nézzük most ezt részenként.

frekvencia¶

Először is, írjunk egy függvényt, ami kap egy stringet és megszámolja benne a betűket egy Map[Char,Int]-be!

Pár talán hasznos tipp: * A `String` sok szempontból úgy viselkedik, mint egy `Vector[Char]`: vannak rá `map`, `filter` stb. metódusok. * Ebből a szempontból kb. a feladat egy `Vector[Char]`-ból készíteni egy `Map[Char,Int]`-et - melyik művelet tűnik erre alkalmasnak?

Hint mutatása

A `foldLeft`, hiszen egész más az eredmény típusa (`Map[Char,Int]`), mint az alaptípus (`Char`). Lehetne éppen `foldRight` is. Tehát: egy kezdetben üres `Map`be kell gyűjtenünk az értékeket, az update pedig egy `(map, char) => map.updated(char, map(char)+1)` lehetne: a Mapünket úgy updateljük, hogy a karakterhez eddig tartozó számot eggyel megnöveljük. Csakhogy ez így kivételt dobna, hiszen alapból nincs kulcs a `map`ben, az `apply` metódus pedig kivételt dob, ha nem létező kulcsot kérünk le, de erre volt való pl. a `getOrElse(char,0)` metódus, ami `0`-t ad vissza, ha a kulcs nem szerepelt a Mapben, egyébként a kulcshoz tartozó értéket:

def countChars( text: String ): Map[Char, Int] =
  text
  .foldLeft[Map[Char,Int]]( Map() ) { //megadtuk a gyűjtő típust és az alapértéket
    (map,char) => map.updated(char, map.getOrElse(char,0) + 1 )
  }

Note: ha egy `Map`ben gyakran használnánk `.getOrElse`-t ugyanazzal a default értékkel, akkor érdemes lehet hívni inkább a `.withDefaultValue( value: V ): Map[K,V]` metódust: ez tartalmilag az eredeti Mapet adja vissza azzal, hogy az `.apply(key)` pontosan úgy fog viselkedni, mint a `.getOrElse( key, value )` , kivétel helyett a megadott default értéket fogja visszaadni. Tehát ez is jó:

def countChars( text: String ): Map[Char, Int] =
  text
  .foldLeft[Map[Char,Int]]( Map().withDefaultValue(0) ) {
    (map,char) => map.updated(char, map(char) + 1 )
  }

Válasz mutatása

algebrai adattípus¶

Implementáljuk a HuffmanTree adattípust! A kép alapján próbáljuk meg meghatározni, hogy hogy épülhet fel.

Hint mutatása

Kétféle fa van a képen (is): * a levelek, nekik van egy `Char` és egy `Int` adattagjuk, * és a belső csúcsok, nekik van egy `Int` adattagjuk és két `HuffmanTree` referencia adattagjuk. Azaz,

1
2
3

HuffmanTree = Leaf + Inner
Leaf        = Char x Int
Inner       = HuffmanTree x Int x HuffmanTree (sorrend mindegy)

sealed trait HuffmanTree{
  def weight: Int
}
case class Leaf( weight: Int, char: Char ) extends HuffmanTree
case class Inner( weight: Int, zero: HuffmanTree, one: HuffmanTree ) extends HuffmanTree

Mivel a traitbe tettünk egy `weight` membert, ezért bármilyen Huffman fának el fogjuk tudni kérni a súlyát; mivel a két case classban így neveztük el a konstruktorban beállított adattagot, ők ezt fogják visszaadni.

Válasz mutatása

SortedSet[HuffmanTree]¶

Az algoritmus egy halmazban kell majd tárolja a fákat és valamilyen kulcs (konkrétan a súlyuk) szerint a legkisebbeket kell tudnia kivenni: erre a célra a SortedSet megfelelő lesz.

Hogyan is hozunk létre olyan, kezdetben üres (és persze továbbra is immutable) SortedSet-et, melyben HuffmanTree-ket akarunk tárolni azok súlya szerint rendezve?

Az első ötletünk lehetne ez:

1	`SortedSet()( (x:HuffmanTree, y:HuffmanTree) => x.weight - y.weight )`

de ez **nem lesz jó**, hiszen lehetséges, hogy két azonos súlyú fánk is van, őket is rendeznünk kell valami alapján, mert ha ez a metódus nullát ad vissza, akkor **egyenlőnek tekinti** a fákat és csak az egyik kerül be a setbe végül, nem ezt akarjuk. Ehelyett pl. írhatunk egy komparátor függvényt, ami a következőt teszi az `x` és `y` huffman fákkal: * ha eltér a súlyuk, legyen a könnyebb a kisebb * különben, ha mindkettő `Leaf`, döntsön a karakter adattag (az már nem lehet egyforma) * különben, ha kettejük közül pontosan az egyik `Leaf`, akkor legyen az a könnyebb * különben, ők két `Inner`node, hasonlítsuk össze mondjuk előbb a `zero` részfa alapján őket rekurzívan, ha az is egyenlő (ez egyébként nem lehetséges ebben az alkalmazásban, mert két fában, amit ténylegesen összehasonlítunk, mindig különbözni fognak a leveleken a betűk, tehát ez már dönteni fog), akkor a `one` részfa alapján:

val comparator: Ordering[HuffmanTree] = {
  (x,y) => if ( x.weight != y.weight ) x.weight - y.weight
  else (x,y) match {
    case (xleaf: Leaf, yleaf: Leaf) => xleaf.char - yleaf.char
    case ( _:Leaf, _ )  => -1  //csak az előjel számít
    case ( _, _:Leaf )  =>  1
    case (Inner(_, xzero, xone), Inner(_, yzero, yone)) => {
      val diffZero = comparator.compare(xzero, yzero)
      if( diffZero != 0 ) diffZero else comparator.compare( xone, yone )
    }
  }
}

val emptySortedSet = SortedSet()(comparator)

Így már jó lesz. Figyeljük meg a következőket: * a `comparator`t implementálnunk kellett, lambdaként nem tudjuk átadni, mert rekurzívan hívja magát * a `SortedSet` konstruktora után **nem egy függvényt** kell átadnunk, hanem egy `Ordering[T]`-t, aminek a `compare` függvénye az, amit implementálunk, ezért van a rekurzív hívásban `.compare` metódus.

Válasz mutatása

Írjunk most egy olyan függvényt, ami egy Map[Char,Int] entryjeiből elkészíti a megfelelő Leaf node-okat és begyűjti őket egy ilyen SortedSet-be!

Ez ismét egy `foldLeft` lesz.

Hint mutatása

def freqsToLeaves( map: Map[Char, Int] ): SortedSet[HuffmanTree] =
  map.foldLeft[SortedSet[HuffmanTree]]( emptySortedSet ) {
    (map, entry) => map + Leaf( entry._2, entry._1 )  //weight, char
  }

Válasz mutatása

faépítés¶

A SortedSet-nek is van size metódusa, head metódusa és kivonni is lehet belőle funkcionális értelemben elemet. Implementáljuk azt az algoritmust, ami addig vesz ki két legkisebb fát és rak be helyettük egyet, amíg egy nem lesz a halmaz mérete!

A szokott módon ez egy ,,ciklus'', tail rekurzív függvényként. Feltesszük, hogy nem üres az input; ha üres stringet akarnánk tömöríteni, azt majd kezeljük az elején.

@tailrec
def makeCodeTree( trees: SortedSet[HuffmanTree] ): HuffmanTree = {
  if( trees.size <= 1 ) trees.head //ekkor kész vagyunk
  else {
    //kivesszük a két legkisebb elemet
    val first  = trees.head        //legkisebb: first
    val trees2 = trees - first    //kivettük
    val second = trees2.head       //ennek a legkisebbje: second
    //rekurzív hívás: kivesszük secondot és betesszük az összeragasztott fákat
    makeCodeTree( trees2 - second + Inner(first.weight + second.weight, first, second) )
  }
}

Válasz mutatása

karakterhez kódszavak¶

Implementáljunk egy olyan függvényt, ami egy HuffmanTree-ből készít (az olvashatóság kedvéért) egy Map[Char, String]-et, ami a fában szereplő karakterekhez rendeli a hozzájuk vezető kódszavakat!

Itt egy olyan rekurzív függvényben érdemes gondolkodni, ami megkap * egy eddig összeépített `Map`et * egy `HuffmanTree`t * és egy az eddig a huffmantreeig vezető prefixet és visszaad egy `Map`et, melyben az eddig szereplőkön kívül a kapott fában lévő karakterek kódjai is hozzáadódnak, mind elé betéve a kapott prefixet. Érdemes lehet matchelni a HuffmanTree-re.

Hint mutatása

def makeMapFromCodeTree( codeTree: HuffmanTree ): Map[Char, String] = {

  def makeMap( codeTree: HuffmanTree, prefix: String, map: Map[Char,String] ): Map[Char, String] = 
  codeTree match {
    case Leaf(_, char)       => map.updated( char, prefix )  //hozzáadtuk ezt a levelet
    case Inner(_, zero, one) => {
      //zerós treet hozzáadjuk, meghosszabbítva a prefixet egy "0"-val
      val plusZero = makeMap( zero, prefix + "0", map )
      //hozzáadjuk a ones treet is, plusz egy "1"-gyel és ezt adjuk vissza
      makeMap( one, prefix + "1", plusZero )
    }
  }

  //meghívjuk a rekurzív függvényünket üres prefixszel és üres Mappal
  makeMap( codeTree, "", Map() )
}

Válasz mutatása

a string elkódolása¶

Implementáljuk a Map[Char,String] alapján minden karaktert a kódjával helyettesítő metódust!

Mivel a `Map[Char,String]` alkalmazható `Char=>String` függvényként is, a `String` meg sok mindenben hasonlít egy `Vector[Char]`-ra, erre gondolhatunk úgy, hogy ezeket az eredményvektorokat kéne egymás után illeszteni - erre van a flatMap:

1	`def encodeContent( text: String, code: Map[Char, String] ) = text flatMap code`

Válasz mutatása

Azt a három bitet is ki kéne írnunk. Írjunk metódust, mely adott szélességre paddolva balról nullákkal kiír egy nemnegatív egész számot binárisan! Használhatjuk például a String.padTo( length: Int, c: Char ) metódust, mely jobbról pakol a stringhez c karaktereket, amíg a hossza el nem éri a length paramétert (persze ahogy mindig, funkcionálisan), és a String.reverse metódust, mely megfordítja a stringet.

def padLeftBinary( n: Int, length: Int ) =
  n.toBinaryString    //bináris alak
  .reverse            //megfordítjuk
  .padTo(length, '0') //a fordított végére pakolunk kellő számú nullát
  .reverse            //visszafordítjuk

Válasz mutatása

Adjuk vissza a teljes elkódolt stringet: a kezdő három biten tárolt ,,trash'' bitek mennyiségét az utolsó nyolc bitből, magát az elkódolt tartalmat, és még annyi nullát, hogy nyolccal osztható legyen a kapott string hossza!

Érdemes előbb kiszámolni a trash bitek mennyiségét, amihez előbb a tényleges content hosszára is szükség van - szerencsére azt már magát ki tudjuk számolni, tehát a hosszát is:

def encodeText( text: String, code: Map[Char, String] ): String = {
  // a content
  val encodedContent = encodeContent( text, code )
  // a hossza
  val contentLength = encodedContent.length
  // kell még három bit, ezt osztani nyolccal, felkerekíteni és megvan, hogy hány byteos
  // tehát nyolcszor annyi bitet fogunk használni
  // felkerekítés: (x+7)/8
  val totalBits = (contentLength + 10) / 8 * 8 //(contentLength + 3 + 7) / 8 * 8
  val trashBits = totalBits - contentLength - 3 //ez 0..7 közt lesz
  // kész is:
  padLeftBinary( trashBits, 3 ) + encodedContent + "".padTo(trashBits, '0')
}

Válasz mutatása

Stringből Byte vektor¶

Írjunk olyan függvényt, mely egy '0', '1' karakterekből álló, 8-cal osztható hosszú Stringből elkészíti azt a Vector[Byte]-ot, melyben nyolcbitenként egy byte-al kódoljuk a stringet!

Használhatjuk hozzá például a következő metódusokat, amik pl. Stringeken is definiálva vannak (meg Vectoron, Listen is):

take(n): az első n elemből (ha van annyi - ha nincs, akkor annyiból, amennyi van) álló részsorozatot adja vissza, pl List(1,4,2,8,5,6).take(3) == List(1,4,2), List(1,2).take(3) == List(1,2)
drop(n): az első n elem eldobásával (ha van annyi - ha nincs, akkor mindet eldobjuk) kapott részsorozatot adja vissza, pl List(1,4,2,8,5,7).drop(2) == List(2,8,5,7) és List(1,2).drop(4) == List()

Persze tetszőleges pl. list listára/vektorra/stringre és n intre list == list.take(n) :: list.drop(n).

Emlékeztetőképp néhány konverziós metódus:

Integer.parseInt( text: String, radix: Int ) : Int egy stringet olvas be mint radix alapú egész számot, pl. Integer.parseInt( "113", 5 ) = 33 (ötös számrendszerben a "113" string ennyit jelent)
Ha v: Int, akkor v.toByte: Byte adja vissza az Int értékét Byte-ban reprezentálva, ha belefér

def compress( text: String ): Vector[Byte] = {

  //a szokásos tailrec az eredménnyel belső függvény
  @tailrec
  def compress( text: String, resultSoFar: Vector[Byte] ): Vector[Byte] = 
  if( text.isEmpty ) resultSoFar // 0 hosszú string, üres, elfogyott
  else {
    //8 hosszú prefix bináris stringet mint kettes számrendszerbeli számot
    //beolvassuk, és byteot csinálunk belőle
    val newByte = Integer.parseInt( text.take(8), 2 ).toByte
    //rekurzió: 8 bittel kevesebbet kell feldolgoznunk, a gyűjtőbe betesszük az új byteot jobbról
    compress( text.drop(8), resultSoFar :+ newByte )
  }

  compress( text, Vector() )
}

Válasz mutatása

az encoder függvény¶

Rakjuk össze, amink eddig van, egy Huffman encoderré: egy függvénnyé, mely kap egy stringet és visszaad (mondjuk) egy Vector[Byte]-ot az elkódolt tartalommal és egy HuffmanTree-t, ami a kódfa, egy párban!

def huffmanEncode( text: String ): (Vector[Byte], HuffmanTree) = {
  val countsMap   = countChars( text )              // a frekvenciák
  val leavesInit  = freqsToLeaves( countsMap )      // a SortedSet, amibe a leveleket rakjuk
  val codeTree    = makeCodeTree( leavesInit )      // a HuffmanTree, amit vissza is fogunk adni
  val dict        = makeMapFromCodeTree( codeTree ) // a Map[Char, String] a bináris stringekkel
  val encodedText = encodeText( text, dict )        // a bináris string, a kezdő három karakterrel és a padding trash
  val byteVector  = compress( encodedText )         // ez meg a másik, amit vissza akarunk adni
  (byteVector, codeTree)                            // kész minden, visszaadtuk
}

Például egy ilyen pipeline esetében a **kompozíció** már egész használható lenne; pl. a codetree elkészítéséhez elég csak chainelni a `countChars`, `freqsToLeaves` és `makeCodeTree` függvényeket pl. így:

1
2
3

val computeCodeTree = countChars _ andThen freqsToLeaves _ andThen makeCodeTree

val codeTree = computeCodeTree( text )

Válasz mutatása

a dekódolás - `Vector[Byte]`-ból vissza a stringet¶

Hogy visszakapjuk az eredeti szövegünket, először írjunk egy függvényt, ami a megkapott bytevektor valahanyadik bitjét visszaadja! Kapjon egy offsetet is, amennyivel tolja el (ez most az alkalmazásunkban 3 lesz, mert a huffman elkódolt szöveg első 3 bitje az, ami nem a szöveg szerves része.

Ahogy Javában is, Scalában is vannak bitenkénti műveletek, pl. `&` a bitenkénti éselés, `<<` a shift left, stb. A [doksiban is látszik](https://www.scala-lang.org/api/current/scala/Byte.html), de fontos lehet: két byte logikai éselése is `Int`et ad már vissza!

Hint mutatása

def getBit( vector: Vector[Byte], index: Int, offset: Int ): Boolean = {
  // hanyadik eleme a vektornak: osztás 8-cal
  val b = vector( (index+offset) / 8 ) //note: Vector-t sem szögletesen indexelünk! apply
  // ezen belül hanyadik bit - a konstrukció úgy ment, hogy a 0. bit kell legyen a legnagyobb helyiérték
  (b & (0x80 >> (index+offset)%8 )) != 0
}

Válasz mutatása

Így, hogy van a biteket elérő függvényünk, írjuk meg a dekódert, ami előállítja az egész input stringet a kódfa és a vektor alapján!

Érdemes lehet egy belső függvényben tailrec végigmenni a contentet elkódoló biteken (kiszámolva előre, hogy meddig kell menni), közben egy csúcsát észben tartva a kódfának, a bit hatására a megfelelő gyerekhez lépni és ha levélhez érünk, berakni a karaktert a kimeneti stringbe, végül ha elfogyott az input, visszaadni a kimeneti stringet.

Hint mutatása

def decode( byteVector: Vector[Byte], codeTree: HuffmanTree ): String = {
  // trash length: első három bit mint hárombites szám
  val trashLength =
    (if ( getBit( byteVector, 0, 0 ) ) 4 else 0) +
      (if ( getBit( byteVector, 1, 0 ) ) 2 else 0) +
      (if ( getBit( byteVector, 2, 0 ) ) 1 else 0)

  // hasznos bitek száma: összes bit, mínusz prefix, mínusz trash
  val contentLength = byteVector.length * 8  - 3 - trashLength

  @tailrec
  def decode( pos: Int, rootNode: Inner, codeNode: Inner, output: String ): String = {
    if( pos == contentLength ) output
    else {
      val direction = getBit( byteVector, pos, 3 )
      val childNode = if (direction) codeNode.one else codeNode.zero
      // rekurzió: pos nő, ha childNode levél, vissza a fa gyökerébe, és ekkor a stringet is bővítjük
      childNode match {
        case Leaf( _, char ) => decode( pos+1, rootNode, rootNode, output + char )
        case inner: Inner    => decode( pos+1, rootNode, inner, output )
      }
    }
  }
  codeTree match {
    case inner: Inner =>   decode( 0, inner, inner, "" )
    case _: Leaf => "" //extrém eset: egyféle karakter van az inputban
  }
}

Válasz mutatása

gyorsteszt¶

Egy módja a gyors tesztelésnek (ha nem teszteltük közben a kódunkat), hogy generálunk egy hosszú szöveget (a lorem ipsum eleje pl. jó lehet) és megnézzük, hogy oda-vissza konvertálással visszakapjuk-e; ha igen, akkor az legalább biztos, hogy a codetree alapján oda-vissza kódolás helyes:

val ( byteVector, huffmanTree ) = huffmanEncode( text )
println( s"Szöveg hossza ${text.length}, byte vektor mérete ${byteVector.length}")
val origText = decode( byteVector, huffmanTree )
println( s"A dekódolt szöveg hossza ${origText.length}, megegyezik az eredetivel? ${origText == text}")

Ha a lipsum megfelelő hosszú elejével teszteljük, akkor ezt kaphatjuk:

1 2	`Szöveg hossza 2487, byte vektor mérete 1319 A dekódolt szöveg hossza 2487, megegyezik az eredetivel? true`

Azaz körülbelül felére tömörödött a string, és a kódolás-dekódolás folyamata megőrizte az információt. (Megjegyzés: erre a konkrét inputra a konkrét szótárt nagyságrendileg kb. 100 byteon el lehet tárolni, tehát még azzal együtt is valódi tömörítésről beszélhetünk.)

Utolsó frissítés: 2021-02-07 23:06:47

14 - Huffman-kódolás¶

az algoritmus¶

példa¶

frekvencia¶

algebrai adattípus¶

SortedSet[HuffmanTree]¶

faépítés¶

karakterhez kódszavak¶

a string elkódolása¶

Stringből Byte vektor¶

az encoder függvény¶

a dekódolás - Vector[Byte]-ból vissza a stringet¶

gyorsteszt¶

a dekódolás - `Vector[Byte]`-ból vissza a stringet¶