Kihagyás

6. gyakorlat

3. ZH

A gyakorlat elején 30 percben kerül megírásra a 3. zh. A feladat(ok) témái:

  • függvények megírása, bemenet/kimenet kezelés nélkül
  • tömbök használata, kezelése

Deklarációk érvényessége

Blokkok

Blokknak nevezünk két kapcsos zárójel { és } közé zárt programrészt. Egy blokkon belül minden változónév (azonosító) csak egyszer deklarálható.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
int main() {
    int szam1;
    {
        int szam2 = 2;
    }
    {
        int szam3 = 3;
        int szam4 = szam1 + szam2 + szam3;  // Ez hibát okoz mivel a szam2
                                            // nincs deklarálva ebben a blokkban
    }
    return 0;
}

Globális és Lokális változók

Globális változó: minden blokkon kívül, a forráskód "legfelső szintjén", a függvények "mellett" deklarált változó. A deklarációját követően mindenhol látszik, mindenhonnan használható.

Lokális változó: valamilyen blokkon (függvényen) belül deklarált változó. Csak az adott blokkon belül látszik (illetve a blokk gyerekblokkjaiban is elérhető).

Feladat (f0014)

Feladat:

Próbáld ki, fordul-e a globals.c program, ha a main függvényben megpróbálod felhasználni a lokalis változót! Mi történik, ha a globalis-t csak a fuggveny() után deklaráljuk?

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
/*
 * Szegedi Tudományegyetem
 * Informatikai Tanszékcsoport
 * Szoftverfejlesztés Tanszék
 *
 * Programozás Alapjai
 */

#include <stdio.h>

int globalis = 0;

int fuggveny(int parameter) {
    int lokalis = 0;
    lokalis += parameter;
    globalis += parameter;
    return lokalis;
}

int main() {
    int i;
    scanf("%d", &i);
    printf("lokalis == %d\nglobalis == %d\n", fuggveny(i), globalis);
    scanf("%d", &i);
    printf("lokalis == %d\nglobalis == %d\n", fuggveny(i), globalis);
    scanf("%d", &i);
    printf("lokalis == %d\nglobalis == %d\n", fuggveny(i), globalis);
    return 0;
}
globals.c

Válaszok

A lokalis változó a fuggveny nevű függvény blokkjában lett deklarálva, így csak abban látható, abban használható. Vagyis a program nem fog lefordulni, mert a main függvényben nem látható a lokalis változó.

Ha a globalis változót a fuggveny nevű függvény után deklaráljuk, akkor hasonló a helyzet: mikor a fordító a függvényben meglátja a globalis nevű azonosítót, akkor (még) nem tudja, hogy ez micsoda, tehát hibát fog jelezni.

Deklarációk

Függvényekben és beágyazott blokkokban létrehozhatunk ugyanolyan nevű változót, mint amilyen korábban valamilyen felsőbb szinten (a kérdéses blokkon kívül) már deklarálva van. Ez az újabb deklaráció el fogja rejteni a korábbi azonos nevű felsőbb szintű változót a kérdéses blokkban:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
#include <stdio.h>

int a = -1;

void fgv() {
    printf("%d\n", a);
}

int main() {
    int a = 0; // ez elrejti a globális "a" változót
    {
        int a = 1; // ez elrejti az eggyel feljebb lévő a változót
        {
            int a = 2; // ez elrejti az eggyel feljebb lévő a változót
            printf("%d\n", a); // 2
            fgv();  // -1
        }
        printf("%d\n", a); // 1
    }
    printf("%d\n", a); // 0
    fgv(); // -1
    return 0;
}
Megjegyzés

A régi-új változó újabb (a kérdéses blokkon belüli) deklarációjában nem kell a változót ugyanolyan típusúnak deklarálnunk, mint felsőbb szinten volt: bármilyen típusúnak deklarálhatjuk.

Óvatosan!

A változók mértéktelen újradeklarálása nagyon megnehezíti a program értelmezését és a hibakeresést. Szóval, csak óvatosan!

Feladat

Próbáld meg fordítás nélkül megtalálni a hibá(ka)t a következő programban, majd javítsd (őket)!

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
int main() {

    int elso;
    elso = 3;
    {
        int masodik;
        elso    = 6
        masodik = 5;
    }
    {
        int harmadik;
        elso    = 9
        masodik = 10;
        harmadik = 8;
    }
    masodik = 15;
    harmadik = 16;
    return 0;
}
Megoldás
  • A 13. sorban a masodik változó nem látható, mert már kívül vagyunk az őt deklaráló blokkon (5-9 sorok).
  • A 16. sorban a masodik változó nem látható, mert már kívül vagyunk az őt deklaráló blokkon (5-9 sorok).
  • A 17. sorban a harmadik változó nem látható, mert már kívül vagyunk az őt deklaráló blokkon (10-15 sorok).

A lokális és globális változók használatára az alábbi videó ad részletes magyarázatot:

Lokál vs global változók

Hibajavítás

Tipp

A gcc-vel való fordításkor mindig használjuk a -Wall kapcsolót. Ez bekapcsolja az összes fordítási warningot (mármint azok figyelését). Nem kötelező, de sokszor segít; rámutat valószínűleg hibás pontokra a programban.

Feladat (f0026)

Feladat:

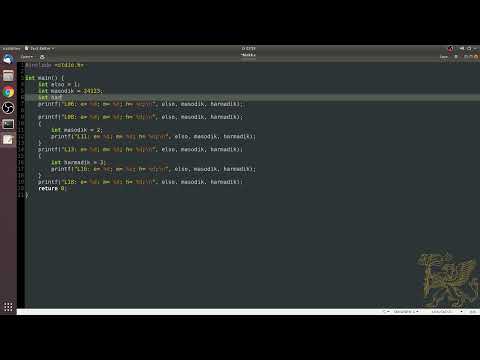
Adott a blokk.c program, amelyben van plusz két blokk. Mindegyik deklarál egy-egy saját változót. Próbáld meg lefordítani a programot, és a hibaüzenet alapján a kiírató utasításokból vedd ki azoknak a változóknak a kiírását (de csak azokét!), amelyekre az adott ponton nem lehet hivatkozni. Maga a kiíratás (az L00 alakú sorszám kiírása) akkor is maradjon meg, ha esetleg mindhárom változó kiírását eltávolítod belőle.

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/*
 * Szegedi Tudományegyetem
 * Informatikai Tanszékcsoport
 * Szoftverfejlesztés Tanszék
 *
 * Programozás Alapjai
 */

#include <stdio.h>

int main() {
    printf("L12: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
    int elso = 1;
    printf("L14: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
    {
        int masodik = 2;
        printf("L17: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
    }
    printf("L19: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
    {
        int harmadik = 3;
        printf("L22: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
    }
    printf("L24: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
    return 0;
}
blokk.c

gcc hibaüzenetek 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
blokk.c: In function ‘main’:
blokk.c:12:43: error: ‘elso’ undeclared (first use in this function)
   12 |     printf("L12: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
      |                                           ^~~~
blokk.c:12:43: note: each undeclared identifier is reported only once for each function it appears in
blokk.c:12:49: error: ‘masodik’ undeclared (first use in this function)
   12 |     printf("L12: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
      |                                                 ^~~~~~~
blokk.c:12:58: error: ‘harmadik’ undeclared (first use in this function)
   12 |     printf("L12: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
      |                                                          ^~~~~~~~
Vagyis a 12. sorban egyik változót sem ismeri. És emlékezzünk a megjegyzésre: minden azonosító miatt csak egyszer szól, amikor először megtalálja.

gcc hibaüzenetek az első javítás után 

1
2
3
4
5
6
7
8
blokk.c: In function ‘main’:
blokk.c:14:49: error: ‘masodik’ undeclared (first use in this function)
   14 |     printf("L14: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
      |                                                 ^~~~~~~
blokk.c:14:49: note: each undeclared identifier is reported only once for each function it appears in
blokk.c:14:58: error: ‘harmadik’ undeclared (first use in this function)
   14 |     printf("L14: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
      |                                                          ^~~~~~~~
És valóban, ha a 12. sor hibáit javítottuk, akkor a 14. sorban találkozik először a két ott még nem deklarált változóval.

gcc hibaüzenetek a második javítás után 

1
2
3
4
5
6
7
8
blokk.c: In function ‘main’:
blokk.c:17:62: error: ‘harmadik’ undeclared (first use in this function)
   17 |         printf("L17: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
      |                                                              ^~~~~~~~
blokk.c:17:62: note: each undeclared identifier is reported only once for each function it appears in
blokk.c:19:49: error: ‘masodik’ undeclared (first use in this function)
   19 |     printf("L19: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
      |                                                 ^~~~~~~
Azután a 17. és 19. sorokban lesz gondja.

gcc hibaüzenetek a harmadik javítás után 

1
2
3
4
5
6
7
8
blokk.c: In function ‘main’:
blokk.c:19:42: error: ‘harmadik’ undeclared (first use in this function)
   19 |     printf("L19: e= %d; h= %d;\n", elso, harmadik);
      |                                          ^~~~~~~~
blokk.c:19:42: note: each undeclared identifier is reported only once for each function it appears in
blokk.c:22:53: error: ‘masodik’ undeclared (first use in this function)
   22 |         printf("L22: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
      |                                                     ^~~~~~~
Ismét a 19. sor, de a másik változó, és a 22. sor.

gcc hibaüzenetek a negyedik javítás után 

1
2
3
4
5
6
7
8
blokk.c: In function ‘main’:
blokk.c:24:49: error: ‘masodik’ undeclared (first use in this function)
   24 |     printf("L24: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
      |                                                 ^~~~~~~
blokk.c:24:49: note: each undeclared identifier is reported only once for each function it appears in
blokk.c:24:58: error: ‘harmadik’ undeclared (first use in this function)
   24 |     printf("L24: e= %d; m= %d; h= %d;\n", elso, masodik, harmadik);
      |                                                          ^~~~~~~~
Most pedig a 24. sor. Ha ezt javítjuk, akkor már lefordul a program.

Megoldás (m0026.c) 

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
/*
 * Szegedi Tudományegyetem
 * Informatikai Tanszékcsoport
 * Szoftverfejlesztés Tanszék
 *
 * Programozás Alapjai
 */

#include <stdio.h>

int main() {
    printf("L12:\n");
    int elso = 1;
    printf("L14: e= %d;\n", elso);
    {
        int masodik = 2;
        printf("L17: e= %d; m= %d;\n", elso, masodik);
    }
    printf("L09: e= %d;\n", elso);
    {
        int harmadik = 3;
        printf("L22: e= %d; h= %d;\n", elso, harmadik);
    }
    printf("L24: e= %d;\n", elso);
    return 0;
}
m0026.c

A hibajavítás folyamatát és gondolatmenetét az alábbi videó is szemlélteti:

Hibajavítás - blokk.c

Feladat (f0029)

Feladat:

Deklarálj és inicializálj egy egész, egy valós és egy karakter változót. Írasd ki mindhárom értékét egészként, valósként és karakterként is! Figyeld meg a fordítási warning-okat és a futási eredményt is!

Lehetséges megoldás (m0029.c) 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
/*
 * Szegedi Tudományegyetem
 * Informatikai Tanszékcsoport
 * Szoftverfejlesztés Tanszék
 *
 * Programozás Alapjai feladat megoldása
 *
 * Gergely Tamás, 2008. őszi félév.
 *
 * Algoritmustervezés/megvalósítás:
 *    Összesen négy kiírató utasításunk lesz, az első helyes, a másik három
 *    pedig egy-egy formátumot használ minden érték kiíratására, ez nyilván
 *    helytelen. A gcc ezt észre fogja venni és szóvá fogja tenni, de ez
 *    csak figyelmeztetés, a fordítást nem akadályozza meg.
 *
 * fordítás:
 *    gcc -Wall -o m0029 m0029.c
 *
 * futtatás:
 *    ./m0029
 */

#include <stdio.h>

int main() {
    int    egesz    = 20151231;
    double valos    = 9.80665;
    char   karakter = 'P';
    printf("e=(%d) v=(%lf) k=('%c')\n",   egesz, valos, karakter);
    printf("e=(%d) v=(%d) k=('%d')\n",    egesz, valos, karakter);
    printf("e=(%lf) v=(%lf) k=('%lf')\n", egesz, valos, karakter);
    printf("e=(%c) v=(%c) k=('%c')\n",    egesz, valos, karakter);
    return 0;
}
Lehetséges válaszok
  • Nem is kapunk mindenhol warningot, csak ha a konverziós specifikáció és a megadott érték egész-valós párt alkot.
  • Az első printf (29. sor) végrehajtásakor nincs probléma, visszakapjuk a 3 változó értékét.
  • A második printf esetén (30. sor), ahol mindent egészként íratunk ki csak az első elem fog stimmelni, a másik kettő nem.
  • A harmadik printf-nél (31. sor) vagy semmi sem stimmel (64 bites architektúrán ez várható), vagy csak a valós érték (32 bites architektúrán).
  • A negyedik printf-nél (32. sor) is furcsa eredményt ad, a 'P' karakter megjelenhet a második értékként (64 bit), de lehet a harmadik helyen is (32 bit); a többi érték mindenesetre nem stimmel.

Feladat (f0066)

Feladat:

Az osszeg-while.c és osszeg-do-while.c programok feladata egy 0 végű egész számsorozat összegének kiszámítása. Mik a programok hibái? Hogyan és miért működnek rosszul ha összeg helyett szorzatot kell számolniuk?

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
/*
 * Szegedi Tudományegyetem
 * Informatikai Tanszékcsoport
 * Szoftverfejlesztés Tanszék
 *
 * Programozás Alapjai
 */

#include <stdio.h>

int main() {
    int x;
    int osszeg = 0;
    while (x != 0) {
        scanf("%d", &x);
        osszeg += x;
    }
    printf("%d\n", osszeg);
    return 0;
}
osszeg-while.c

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
/*
 * Szegedi Tudományegyetem
 * Informatikai Tanszékcsoport
 * Szoftverfejlesztés Tanszék
 *
 * Programozás Alapjai
 */

#include <stdio.h>

int main() {
    int x;
    int osszeg = 0;
    do {
        scanf("%d", &x);
        osszeg += x;
    } while (x != 0);
    printf("%d\n", osszeg);
    return 0;
}
osszeg-do-while.c

Lehetséges válaszok
  • Az első program 14. sorában az x változót úgy használjuk fel a while feltételében, hogy korábban még nem inicializáltuk. Ilyenkor a memória állapotától függő, véletlenszerű értéket vesz fel az x változó, így előfordulhat például, hogy ha ez az érték éppen 0, akkor a ciklus le se fut.
  • A beolvasott értéket mindkét programban mindenképpen hozzáadjuk az összeghez, mielőtt ellenőriznénk, hogy a végjel volt-e az. Mivel 0 a végjel, összeadásnál ez nem okoz gondot, szorzásnál viszont lenullázná a végeredményt.

Feladat (f0276)

Feladat:

A teljesítménytúrák olyan szervezett túrák, amelyeken egy adott útvonalat kell megadott időn belül teljesíteni. Az indulásra (a torlódás elkerülése végett) egy több órás időintervallumot szokás megadni. Az útvonalon ellenőrző pontokat szokás felállítani. A Magyar Természetbarát Szövetség Gyalogos teljesítménytúrák szervezési szabályzata szerint az egyes ellenőrzőpontok nyitvatartását úgy kell meghatározni, hogy a legfeljebb 6km/h és legalább 4km/h sebességgel haladó, a rajtra megadott időintervallumban induló túrázók mindenéppen nyitott ellenőrzőpontokat találjanak.

A feladat egy olyan program elkészítése, amely segít meghatározni az egyes pontok (beleértve a cél, azaz az utolsó ellenőrzőpont) nyitvatartását. Az input két időpont óra:perc pontossággal, az indulás legkorábbi és legkésőbbi lehetséges időpontja; majd több valós szám, amik sorban az egyes ellenőrzőpontok közötti távolságokat jelentik (km-ben). Az utolsó érték 0, ez jelzi, hogy nincs több ellenőrzőpont. A program kimenete az egyes ellenőrző pontokhoz tartozó nyitási és zárási időpont, negyedórára "kiterjesztve" a túrázóknak kedvező módon. Ez azt jelenti, hogy ha egy adott ellenőrzőponhoz például a 9:13:19-11:02:11 -es időpontok tartoznának, akkor az ellenőrzőpont 9:00-től 11:15-ig lesz nyitva. Az ellenőrzőpontok száma (a céllal együtt) nem lesz több 20-nál.

Megvalósítás:

A programban az időpontokat egy olyan függvény számolja, amelyiknek négy paramétere van: a rajt kezdőidőpontja, a rajt végidőpontja, az ellenőrzőpontok száma, és egy valós tömb, amely a ellenőrzőpontok rajttól mért távolságát tartalmazza (km-ben). A kiíratást ez a függvény végezheti.

A tömb feltöltéséért, az input kezeléséért a főprogram feleljen.

Ötletek
  • Az időpontra érdemes struct-ot csinálni, másodperc alapon.
  • Fix 20 méretű tömböt elég foglalni.
  • Tömbfeltöltés: az inputban relatív távolság van megadva, a tömbben abszolút kell majd.
  • Jól jöhet egy olyan függvény, ami megadja, hogy egy útszakaszt valamilyen sebességgel mennyi idő alatt lehet megtenni.
  • Az időpont két irányban való "kiterjesztését" végezheti egy-egy külön függvény.
  • Érdemes az időpontok összeadására is külön függvényt írni.
  • Egy adott ellenőrzőpontnál a rajt kezdő- illetve végidőpontja alapján ki kell számolni, hogy 6 illetve 4 km/h sebességgel mikor érhetnek oda, és ezt lefelé illetve felfelé negyedórára kell kerekíteni.
Lehetséges megoldás (m0276.c) 
 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
/*
 * Szegedi Tudományegyetem
 * Informatikai Tanszékcsoport
 * Szoftverfejlesztés Tanszék
 *
 * Programozás Alapjai feladat megoldása
 *
 * Gergely Tamás, 2019. őszi félév.
 *
 * fordítás:
 *    gcc -o m0276 m0276.c
 *
 * futtatás:
 *    ./m0276
 */

#include <stdio.h>

#define N 20
#define KMP 900

#define min_seb 4.0
#define max_seb 6.0

typedef struct {
    int ora;
    int perc;
    int mp;
} ido_t;

int ido_to_int(ido_t i) {
    return 3600 * i.ora + 60 * i.perc + i.mp;
}

ido_t int_to_ido(int i) {
    ido_t retval = {0, 0, 0};
    retval.ora = i / 3600;
    i %= 3600;
    retval.perc = i / 60;
    retval.mp = i % 60;
    return retval;
}

ido_t ido_le(ido_t idopont) {
    int sec = ido_to_int(idopont);
    sec = KMP * (sec / KMP);
    return int_to_ido(sec);
}

ido_t ido_fel(ido_t idopont) {
    int sec = ido_to_int(idopont);
    sec = (KMP * (1 + ((sec-1) / KMP)));
    return int_to_ido(sec);
}

ido_t ido_add(ido_t a, ido_t b) {
    return int_to_ido(ido_to_int(a) + ido_to_int(b));
}

ido_t ido(double s, double v) {
    int sec = 3600.0 * s / v; // Itt implicit double -> int átalakítás (csonkolás, alsó egészrész) történik
    return int_to_ido(sec);
}

void nyitvatartas(ido_t kezd, ido_t veg, int n, double p[]) {
    for (int i = 0; i < n; ++i) {
        ido_t nyit, zar;
        nyit = ido_le(ido_add(kezd, ido(p[i], max_seb)));
        zar  = ido_fel(ido_add(veg, ido(p[i], min_seb)));
        printf("A(z) %d. ellenőrzőpont %2d:%02d és %2d:%02d között van nyitva.\n", i+1, nyit.ora, nyit.perc, zar.ora, zar.perc);
    }
}

int main() {
    ido_t k = {0,0,0}, v = {0,0,0};
    double s, ts = 0.0, p[N];
    int i;
    i = 0;
    scanf("%d:%d", &(k.ora), &(k.perc));
    scanf("%d:%d", &(v.ora), &(v.perc));
    scanf("%lf", &s);
    while (s != 0.0) {
        ts += s;
        p[i++] = ts;
        scanf("%lf", &s);
    }
    nyitvatartas(k, v, i, p);
    return 0;
}

Feladatok

Feladat (f0034)

Problémafelvetés:

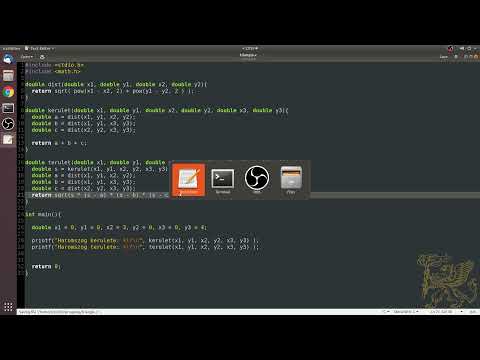
Írj egy programot ami három kétdimenziós koordináta-párból kiszámítja egy háromszög kerületét és területét!

Specifikáció:

A program inputja három pár valós szám, amelyek \(x_1, y_1, x_2, y_2, x_3, y_3\) sorrendben a háromszög \(A(x_1,y_1), B(x_2,y_2)\) és \(C(x_3,y_3)\) csúcsainak koordinátái. A program outputja két sor. Az elsőben a "T = " szöveg után a háromszög területe, a második sorban a "K = " szöveg után a háromszög kerülete szerepel. Mindkét számot 10 karakteren jobbra igazítva 3 tizedesjegy pontossággal kell kiíratni. A beolvasás előtt a program elején ki kell írni egy rövid tájékoztatót arról, hogy a program milyen adatot kér be.

Algoritmustervezés:

A terület és kerület kiszámítására készítsünk egy-egy függvényt, amik a három oldalhosszból kiszámolják a megfelelő adatokat. Az oldalhosszakat pedig a pontok páronkénti távolságának kiszámításával kapjuk meg, amit szintén egy függvény végezhet el. A főprogramra így a be- és kimenet kezelése, valamint a függvények közötti adatáramlás megvalósítása marad.

Lehetséges megoldás (videó)

A specifikációtól eltérve, de a következő videó lényegében ezt a feladatot oldja meg:

traingle_ter_ker

Feladat (f0038)

Problémafelvetés:

Írj egy programot ami az él hosszából kiszámolja mind az 5 szabályos test (tetraéder, hexaéder, oktaéder, dodekaéder, ikozaéder) felszínét és térfogatát, majd html formátumban táblázatos formában (5 sor, soronként a test neve, felszíne, térfogata) 6 tizedesjegy pontossággal kiírja az adatokat.

Megvalósítás:

A html fájl, mely egyetlen táblázatot tartalmaz, valahogy így néz ki:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
<html><body>
<table><tr>
<td>Ez a táblázat első sorának első oszlopa</td>
<td>Ez a táblázat első sorának 2. oszlopa</td>
<td>Ez a táblázat első sorának 3. oszlopa</td>
</tr><tr>
<td>Ez a táblázat második sorának 1. oszlopa</td>
<td>2. sor 2. oszlop</td>
<td>2/3</td>
</tr><tr>
<td>És ez hasonló</td>
<td>módon mehet</td>
<td>tovább</td>
</tr></table>
</body></html>

A sortörések helye nem számít, de minden nyitó <tag>-hez kell egy lezáró </tag> is, ráadásul a zárójelezési szabályoknak megfelelően. A <html> a html oldalt, a <body> a konkrét tartalmat, a <table> a táblázatot, a <tr> egy sort, a <td> pedig a soron belül egy cellát jelöl. Ha a program kimenetét a shell-ben átirányítod (a > segítségével) egy fájlba, az eredményt meg tudod nézni egy böngészővel.

Feladat (f0054)

Problémafelvetés:

Egy facölöp egyik végét csonka kúp alakúra, másik végét forgáskúp alakúra formálták. (Így egy forgástestet kaptunk.) A középső, forgáshenger alakú rész hossza \(L_1\) cm és átmérője \(D_1\) cm. A csonka kúp alakú rész magassága \(L_2\) cm, a csonka kúp fedőlapja pedig \(D_2\) cm átmérőjű. Az elkészült cölöp teljes hossza \(L\) cm. Az elkészült cölöpök felületét vékony lakkréteggel vonják be.

  • a) Hány \(m^3\) fára volt szükség N darab cölöp gyártásához, ha az egyes cölöpök gyártáskor négyzetes hasáb formájú gerendákból indultak ki, melyek hossza pontosan \(L\), szélessége és magassága pedig \(D_1\)?
  • b) A felhasznált alapanyag hány százaléka hulladék?
  • c) Hány \(m^2\) felületet kell belakkozni, ha N cölöpöt gyártottak?

A program kimenete egy HTML oldal, melyben egy két oszlopos és három soros táblázat van. Az első oszlop három sorában az "alapanyag", "hulladék" és "lakk" feliratok, a második oszlop soraiban pedig a megfelelő kiszámított értékek, mértékegységgel ellátva. A végeredmény böngészőben megjelenítve valami ilyesmi legyen:

1
2
3
4
5
+-----------+-----------+
| Alapanyag | 3.125 m^3 |
| Hulladék  | 22.1%     |
| Lakk      | 6.333 m^2 |
+-----------+-----------+
Feladat (f0166)

Problémafelvetés:

Készíts egy programot, amely egy tetszőleges nagyságú (maximum 9999 jegyű) számról a jól ismert oszthatósági szabályok felhasználásával eldönti, hogy a szám osztható-e a [2..12] intervallumba eső számok bármelyikével.

Algoritmustervezés/Megvalósítás:

A felhasználható oszthatósági szabályok:

  • 2: az utolsó számjegy oszthatóságát kell vizsgálni
  • 3: a számjegyek összegének oszthatóságát kell vizsgálni
  • 4: az utolsó két számjegy által alkotott szám oszthatóságát kell vizsgálni
  • 5: az utolsó számjegy oszthatóságát kell vizsgálni
  • 6: 2-vel és 3-mal való oszthatóságot kell vizsgálni
  • 7: a szám végétől (jobb szélétől) kezdve az eleje felé hármasával csoportosítva a számjegyeket a kapott háromjegyű számok alternáló összegének oszthatóságát kell vizsgálni
  • 8: az utolsó három számjegy által alkotott szám oszthatóságát kell vizsgálni
  • 9: a számjegyek összegének oszthatóságát kell vizsgálni
  • 10: az utolsó számjegy oszthatóságát kell vizsgálni
  • 11: a számjegyek alternáló összegének oszthatóságát kell vizsgálni
  • 12: 3-mal és 4-gyel való oszthatóságot kell vizsgálni

Egy 9999 jegyű szám nem fér bele a C nyelv egyetlen létező egész adattípusának értékkészletébe sem, így számként nem tudjuk egyben kezelni. Sztringként viszont minden további nélkül eltárolható. Ezek után az oszthatósági szabályoknak megfelelően kell leellenőrízni a sztringet. Érdemes az egyes szabályokat külön-külön függvénykben úgy megvalósítani, hogy az oszthatóság ellenőrzése a sztringet ne módosítsa. A függvények nem kiírják az eredményt (ez a főprogram, vagy egy kifejezetten a kiírást szolgáló függvény feladata lenne), hanem egy logikai értéket adnak vissza.

Lehetséges megoldás (m0166.c) 
  1
  2
  3
  4
  5
  6
  7
  8
  9
 10
 11
 12
 13
 14
 15
 16
 17
 18
 19
 20
 21
 22
 23
 24
 25
 26
 27
 28
 29
 30
 31
 32
 33
 34
 35
 36
 37
 38
 39
 40
 41
 42
 43
 44
 45
 46
 47
 48
 49
 50
 51
 52
 53
 54
 55
 56
 57
 58
 59
 60
 61
 62
 63
 64
 65
 66
 67
 68
 69
 70
 71
 72
 73
 74
 75
 76
 77
 78
 79
 80
 81
 82
 83
 84
 85
 86
 87
 88
 89
 90
 91
 92
 93
 94
 95
 96
 97
 98
 99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
/*
 * Szegedi Tudományegyetem
 * Informatikai Tanszékcsoport
 * Szoftverfejlesztés Tanszék
 *
 * Programozás Alapjai
 *
 * Gergely Tamás, 2017. őszi félév.
 *
 * fordítás:
 *    gcc -o m0166 m0166.c
 *
 * futtatás:
 *    ./m0166
 */

#include <stdio.h>

int o2(char* sz) {
    int i, s = 0;
    for (i = 0; sz[i] != 0; ++i);
    if (i > 0) {
        s += (sz[--i] - '0');
    }
    return s % 2 == 0;
}

int o3(char* sz) {
    int i, s = 0;
    for (i = 0; sz[i] != 0; ++i) {
        s += sz[i] - '0';
    }
    return s % 3 == 0;
}

int o4(char* sz) {
    int i, s = 0;
    for (i = 0; sz[i] != 0; ++i);
    if (i > 0) {
        s += (sz[--i] - '0');
        if (i > 0) {
            s += 10 * (sz[--i] - '0');
        }
    }
    return s % 4 == 0;
}

int o5(char* sz) {
    int i, s = 0;
    for (i = 0; sz[i] != 0; ++i);
    if (i > 0) {
        s += (sz[--i] - '0');
    }
    return s % 5 == 0;
}

int o6(char* sz) {
    return o2(sz) && o3(sz);
}

int o7(char* sz) {
    int i, s = 0;
    for (i = 0; sz[i] != 0; ++i);
    while (i > 0) {
        int t = 0;
        if (i > 0) {
            t += (sz[--i] - '0');
            if (i > 0) {
                t += 10 * (sz[--i] - '0');
                if (i > 0) {
                    t += 100 * (sz[--i] - '0');
                }
            }
        }
        s = t - s;
    }
    return s % 7 == 0;
}

int o8(char* sz) {
    int i, s = 0;
    for (i = 0; sz[i] != 0; ++i);
    if (i > 0) {
        s += (sz[--i] - '0');
        if (i > 0) {
            s += 10 * (sz[--i] - '0');
            if (i > 0) {
                s += 100 * (sz[--i] - '0');
            }
        }
    }
    return s % 8 == 0;
}

int o9(char* sz) {
    int i, s = 0;
    for (i = 0; sz[i] != 0; ++i) {
        s += sz[i] - '0';
    }
    return s % 9 == 0;
}

int o10(char* sz) {
    return o5(sz) && o2(sz);
}

int o11(char* sz) {
    int i, s = 0;
    for (i = 0; sz[i] != 0; ++i) {
        s = sz[i] - '0' - s;
    }
    return s % 11 == 0;
}

int o12(char* sz) {
    return o4(sz) && o3(sz);
}

int main() {
    char szam[10000];
    scanf("%9999s", szam);
    printf("A szám%s osztható 2-vel.\n",    o2(szam) ? "" : " nem");
    printf("A szám%s osztható 3-mal.\n",    o3(szam) ? "" : " nem");
    printf("A szám%s osztható 4-gyel.\n",   o4(szam) ? "" : " nem");
    printf("A szám%s osztható 5-tel.\n",    o5(szam) ? "" : " nem");
    printf("A szám%s osztható 6-tal.\n",    o6(szam) ? "" : " nem");
    printf("A szám%s osztható 7-tel.\n",    o7(szam) ? "" : " nem");
    printf("A szám%s osztható 8-cal.\n",    o8(szam) ? "" : " nem");
    printf("A szám%s osztható 9-cel.\n",    o9(szam) ? "" : " nem");
    printf("A szám%s osztható 10-zel.\n",  o10(szam) ? "" : " nem");
    printf("A szám%s osztható 11-gyel.\n", o11(szam) ? "" : " nem");
    printf("A szám%s osztható 12-vel.\n",  o12(szam) ? "" : " nem");
    return 0;
}
Feladat (f0175)

Feladat:

Egészítsd ki úgy a simplemaths.c programot, hogy megfelelően működjön. A program feladata az inputon soronként megadott egyszerű matematikai műveletek elvégzése lenne. A függvények megvalósítása a main() függvény után következzen. A program az alábbi műveleteket ismerné (ahol E nemnegatív decimális egész, V pedig valós számokat jelöl:

  • fact E : kiszámolja E faktoriálisát
  • sqr V : kiszámolja V négyzetét
  • cube V : kiszámolja V köbét
  • add V1, V2 : kiszámolja a V1 + V2 összeget
  • sub V1, V2 : kiszámolja a V1 - V2 különbséget
  • mul V1, V2 : kiszámolja a V1 * V2 szorzatot
  • per V1, V2 : kiszámolja a V1 / V2 hányadost
  • div E1, E2 : kiszámolja az E1 / E2 egészosztás hányadosát
  • mod E1, E2 : kiszámolja az E1 / E2 egészosztás maradékát
  • exit : kilép a programból

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
/*
 * Szegedi Tudományegyetem
 * Informatikai Tanszékcsoport
 * Szoftverfejlesztés Tanszék
 *
 * Programozás Alapjai
 */

#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define N 64

int main() {
    char buff[N];
    while (fgets(buff, N, stdin) != NULL) {
        unsigned int tmpi1, tmpi2;
        double tmpd1, tmpd2;
        if (strncmp(buff, "exit", 4) == 0) {
            break;
        } else if (sscanf(buff, "fact %u", &tmpi1) == 1) {
            printf("= %u\n", fact(tmpi1));
        } else if (sscanf(buff, "sqr %lf", &tmpd1) == 1) {
            printf("= %lf\n", sqr(tmpd1));
        } else if (sscanf(buff, "cube %lf", &tmpd1) == 1) {
            printf("= %lf\n", cube(tmpd1));
        } else if (sscanf(buff, "add %lf %lf", &tmpd1, &tmpd2) == 2) {
            printf("= %lf\n", add(tmpd1, tmpd2));
        } else if (sscanf(buff, "sub %lf %lf", &tmpd1, &tmpd2) == 2) {
            printf("= %lf\n", sub(tmpd1, tmpd2));
        } else if (sscanf(buff, "mul %lf %lf", &tmpd1, &tmpd2) == 2) {
            printf("= %lf\n", mul(tmpd1, tmpd2));
        } else if (sscanf(buff, "per %lf %lf", &tmpd1, &tmpd2) == 2) {
            printf("= %lf\n", per(tmpd1, tmpd2));
        } else if (sscanf(buff, "div %u %u", &tmpi1, &tmpi2) == 2) {
            printf("= %u\n", divide(tmpi1, tmpi2));
        } else if (sscanf(buff, "mod %u %u", &tmpi1, &tmpi2) == 2) {
            printf("= %u\n", modulo(tmpi1, tmpi2));
        } else {
            printf("Érvénytelen parancs!\n");
        }
    }
    return 0;
}
simplemaths.c

További gyakorló feladatok

Feladat (f0027)

Amikor elindítjuk a programunkat, akkor a linux tulajdonképpen meghívja, kiértékeli a main() függvényt. A main által kiszámított értéket a "Volt-e hiba?" kérdésre adott válaszként értelmezi. C-ben a 0 érték logikailag hamis értéket jelent, ezért a linux a 0 értéket fogja jó futásként értelmezni ("NEM volt hiba."). C-ben a nem 0 érték logikailag igazként értelmezendő, így a linux az 1 visszatérési értéket futási hibaként kezeli ("IGEN, volt hiba.").

Feladat:

Írd meg a HelloWorld programodat kétféleképpen: a main függvény végén a return utasítás az egyik esetben 0, a másik esetben 1 értéket adjon vissza. (A kiíratás is lehet "Hello 0!" és "Hello 1!", hogy futtatáskor láthatóbb legyen az eredmény, de a program működését ez lényegében nem befolyásolja.) A programokat fordítsd le hello0 és hello1 néven. Mi az eredménye az alábbi linux parancsoknak?

1
2
3
4
5
6
$ ./hello0 ; ./hello0
$ ./hello1 ; ./hello1
$ ./hello0 && ./hello0
$ ./hello1 && ./hello1
$ ./hello0 || ./hello0
$ ./hello1 || ./hello1
Feladat (f0096)

Problémafelvetés:

Írj olyan programot, mely kiírja az összes kétoperandusú logikai művelet (==, !=, <, <=, >, >=, &&, ||) értékét egy html oldalon belül elhelyezett táblázatban. A kimenet egy ehhez hasonló, de html-ben kódolt táblázat, természetesen a megfelelő értékekkel kitöltve:

1
2
3
4
5
6
7
8
+---+---+----+----+---+----+---+----+----+----+
| a | b | == | != | < | <= | > | >= | && | || |
+---+---+----+----+---+----+---+----+----+----+
| H | H |  I |  . | . |  . | . |  . |  . |  H |
| H | I |  H |  . | . |  . | . |  . |  . |  I |
| I | H |  H |  . | . |  . | . |  . |  . |  I |
| I | I |  I |  . | . |  . | . |  . |  . |  I |
+---+---+----+----+---+----+---+----+----+----+
Feladat (f0105)

Problémafelvetés:

Lakásra gyűjtünk. Havonta félre tudunk tenni X összeget, amely a tőkét gyarapítja. A tőkénkre a bank K% éves kamattal havonta fizet kamatot (minden hónapban (K/12)%-ot) és ezt hozzáírja a tőkéhez. A tőkénkhez szintén a hónap végén az állam is hozzáteszi az adott havi X befizetésünk A%-át, de maximum M összeget. Hány hónapig kell félretennünk, hogy a hónap végére összegyűlt tőke fedezze a lakás Y árát? Az X és Y pozitív valós érték (valamennyit félre tudunk tenni havonta, és a lakást nem adják ingyen), a K, A, és M pedig nemnegatív valós értékek (vagyis lehet, hogy sem kamatot, sem állami támogatást nem kapunk, de a tőkénk nem csökken).

Feladat (f0106)

Problémafelvetés:

Lakásra gyűjtünk. Havonta félre tudunk tenni X összeget, amely a tőkét gyarapítja. A tőkénkre a bank K% éves kamattal havonta fizet kamatot (minden hónapban (K/12)%-ot) és ezt hozzáírja a tőkéhez. A tőkénkhez szintén a hónap végén az állam is hozzáteszi az adott havi X befizetésünk A%-át, de maximum M összeget. A hónap végén a bank a tőkéből levon egy fix V számlavezetési díjat. Hány hónapig kell félretennünk, hogy a hónap végére összegyűlt tőke fedezze a lakás eredetileg Y, de havonta I% inflációval növelt árát? (Az infláció csak a lakásárra vonatkozik.) Az X és Y pozitív valós érték (valamennyit félre tudunk tenni havonta, és a lakást nem adják ingyen), a K, A, M, és I nemnegatív valós értékek (vagyis lehet, hogy nincs kamat, állami támogatást sem kapunk, de a bank is vezetheti ingyen a számlánkat), az I pedig valós érték (azaz megengedett a negatív infláció). Egyáltalán, adott értékek mellett van-e legalább matematikai esélyünk összeszedni a pénzt?

Feladat (f0114)

Problémafelvetés:

Készíts egy programot, ami a fogyasztás és a hónap alapján kiszámítja az adott hónapban fizetendő gázárat, ha tudjuk, hogy a gázár sávosan változik: (1) az első 1000 egység ára 100¤/egység; (2) a második 1000 egység ára már 200¤/egység; (3) egyébként a gázár 300¤/egység; és (4) a téli hónapokban (nov, dec, jan, feb) a gázárat 1.2 -vel szorozzák.

Feladat (f0172)

Problémafelvetés:

Készíts olyan programot, mely előállítja egy adott intervallumba eső véletlen számokból álló számsorozat diszkrét differenciáját.

Specifikáció:

Az input három egész szám: N, MIN és MAX. N az elkészítendő minta sorozat elemszáma, MIN a sorozat elemeinek alsó, MAX a felső korlátja (mindkét korlát előfordulhat a sorozatban).

Az output egyetlen sor, az N értéke majd további N darab egész érték, egy-egy szóközzel elválasztva. Ez utóbbiak a minta sorozatból számolt diszkrét differencia sorozat elemei.

Algoritmustervezés/Megvalósítás:

A diszkrét differencia egy a mintával egyező hosszú vektor, ahol az első elem megegyezik a minta első elemével, az i. elem pedig a minta i. és i-1. elemének különbsége.

Feladat (f0173)

Problémafelvetés:

Készíts olyan programot, mely egy sorozat diszkrét differenciájából előállítja az eredeti sorozatot.

Specifikáció:

Az input egy N egész szám, a sorozat mérete, majd további N darab egész érték, a diszkrét differencia sorozat elemei.

Az output egyetlen sor, benne a diszkrét differencia sorozatból visszaállított eredeti minta sorozat elemei, egy-egy szóközzel elválasztva.

Algoritmustervezés/Megvalósítás:

A diszkrét differencia egy a mintával egyező hosszú vektor, ahol az első elem megegyezik a minta első elemével, az i. elem pedig a minta i. és i-1. elemének különbsége.

Feladat (f0176)

Problémafelvetés:

Szükségünk lenne egy programra, amely térbeli és síkbeli geometriai alakzatok kerületét, területét, felszínét, térfogatát, és egyes egyéb jellemzőit képes kiszámolni az alakzat néhány adata alapján. A program interaktív, soronként lehet neki egy kérdést megadni a megfelelő paraméterekkel, amire "válaszol". A program által ismerendő kérdések (ahol a % egy valós, nemnegatív értéket jelöl):

  • circ A % : egy kör területe a sugara alapján
  • circ C % : egy kör kerülete a sugara alapján
  • square A % : egy négyzet területe az oldalhossza alapján
  • square C % : egy négyzet kerülete az oldalhossza alapján
  • square D % : egy négyzet átlója az oldalhossza alapján
  • rect A % % : egy téglalap területe a két oldalhossza alapján
  • rect C % % : egy téglalap kerülete a két oldalhossza alapján
  • rect D % % : egy téglalap átlója a két oldalhossza alapján
  • tri A % : egy szabályos háromszög területe az oldalhossza alapján
  • tri C % : egy szabályos háromszög kerülete az oldalhossza alapján
  • pent A % : egy szabályos ötszög területe az oldalhossza alapján
  • pent C % : egy szabályos ötszög kerülete az oldalhossza alapján
  • pent D % : egy szabályos ötszög átlója az oldalhossza alapján
  • hex A % : egy szabályos hatszög területe az oldalhossza alapján
  • hex C % : egy szabályos hatszög kerülete az oldalhossza alapján
  • hex d % : egy szabályos hatszög kisátlója az oldalhossza alapján
  • hex D % : egy szabályos hatszög nagyátlója az oldalhossza alapján
  • sphere V % : egy gömb térfogata a sugara alapján
  • sphere A % : egy gömb felszíne a sugara alapján
  • cube A % : egy kocka térfogata az élhossza alapján
  • cube V % : egy kocka felszíne az élhossza alapján
  • cube D % : egy kocka testátlója az élhossza alapján
  • brick V % % % : egy téglatest térfogata a három élhossza alapján
  • brick A % % % : egy téglatest felszíne a három élhossza alapján
  • brick D % % % : egy téglatest testátlója a három élhossza alapján
  • tetra V % : egy szabályos tetraéder térfogata az élhossza alapján
  • tetra A % : egy szabályos tetraéder felszíne az élhossza alapján
  • hexa V % : egy szabályos hexaéder térfogata az élhossza alapján
  • hexa A % : egy szabályos hexaéder felszíne az élhossza alapján
  • octa V % : egy szabályos oktaéder térfogata az élhossza alapján
  • octa A % : egy szabályos oktaéder felszíne az élhossza alapján
  • dodeka V % : egy szabályos dodekaéder térfogata az élhossza alapján
  • dodeka A % : egy szabályos dodekaéder felszíne az élhossza alapján
  • ikoza V % : egy szabályos ikozaéder térfogata az élhossza alapján
  • ikoza A % : egy szabályos ikozaéder felszíne az élhossza alapján
  • exit : kilép a programból

Kapcsolódó linkek

Utolsó frissítés: 2023-10-20 07:16:25